仭峆惎偺弌杤帪崗偺寁嶼
偙傟傑偱偺峫偊曽偱丄摿掕偺抧堟偺峆惎偺弌杤帪崗偑寁嶼偱偒傑偡丅
愒摴嵗昗仺抧暯嵗昗偺曄姺幃(3)偺h=0亱偲抲偄偨応崌丅
0 = sin冋sin兟+cos冋cos兟cosH0
cosH0 = - tan兟tan冋
偙偙偱偺H0偼丄揤懱偑弌尰偟偰撿拞偡傞丄傑偨偼撿拞偟偰杤偡傞帪娫傪峆惎帪娫偱昞偟偨傕偺偱偡丅
抧暯慄忋晅嬤偵偁傞惎偼丄嬻婥偺孅愜偵傛傝晜偒忋偑偭偰尒偊傑偡丅
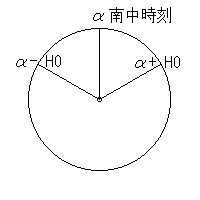
偙傟傪戝婥嵎偲屇傃傑偡丅偙偺妏搙偼崅偝0亱(h=0亱)偵偍偄偰栺35'偱偡丅
偙偺妏搙偩偗丄峆惎帪傪曗惓偡傞昁梫偑偁傝傑偡丅偙偺帪妏傪嚈H偲偡傞偲丅
嚈H=R/(cos冋cos兟sinH0)
R:戝婥嵎丂35'
冋:娤應抧偺堒搙
兟:峆惎偺愒堒
H0偲嚈H偑傢偐傞偲峆惎偑弌杤偡傞峆惎帪偼埲壓偲側傝傑偡丅
峆惎偑弌尰偡傞抧曽峆惎帪= 兛 - h0 - 嚈H
峆惎偑杤偡傞抧曽峆惎帪丂= 兛 + h0 + 嚈H
偙偺峆惎帪傪丄媮傔偨偄擔晅偺帪崗偵曄姺偡傟偽俷俲丅
峆惎偑弌杤偡傞曽埵A0
sinA0 = -cos兟sin(亇(h0 + 嚈H))
cosA0 = sin兟 / cos冋
亇(h0 + 嚈H):弌尰帪崗丂亅丂丄杤帪崗丂亄
仭椺戣
俀侽侽侽擭侾寧侾擔偺嫗搒乮宱搙丗搶宱135亱44'丄堒搙丗杒堒35亱01'乯偵偍偗傞僔儕僂僗乮愒宱丗6h45.1m丄愒堒丗-16亱43'乯偺弌杤帪崗丄弌杤帪偺曽埵
cosH0 = - tan兟tan冋
= - tan(-16亱43') x tan(35亱01')
= - (-0.30033) x 0.70064
= 0.21042
H0 = 77.853亱
= 5h 11.4m
嚈H = R/(cos冋cos兟sinH0)
= 35/60/(cos (35亱01') x cos(-16亱43') x sin(77.853亱) )
= 0.58333/(0.81899 x 0.95774 x 0.97761)
= 0.76072亱
= 0h 3.0m
弌尰帪崗乮峆惎偑弌尰偡傞抧曽峆惎帪乯
兛 - h0 - 嚈H
= 6h 45.1m - 5h 11.4m - 0h 3.0m
= 1h 30.7m
2000擭1寧1擔0帪UT偵偍偗傞僌儕僯僢僕峆惎帪
2000擭1寧1擔0帪UT偺弨儐儕僂僗擔丅棟壢擭昞傛傝丅寁嶼傕偱偒傑偡丅
MJD = 51544.0
兤G0 = 24hx(0.67239亄1.00273781x(MJD-40000.0)) = 6.6640h
(0.67239亄1.00273781x(MJD-40000.0))偺彮悢揰埲壓偺傒巊梡丅
6.6640h = 6h 39.8m
2000擭1寧1擔0帪UT偵偍偗傞嫗搒偺抧曽峆惎帪
嫗搒偺宱搙丂搶宱135亱44' = 9h 2.9m
兤0 = 兤G0 - 兩
= 6h 39.8m - (-9h 2.9m)
= 15h 42.7m
峆惎偑弌尰偡傞抧曽峆惎帪傪悽奅帪UT傊曄姺
1h 30.7m=1.5117h
15h 42.7m=15.7117h
1.5117h - 15.7117h = -14.200h
亅乮儅僀僫僗乯偵側偭偨偨傔+24h
9.8000h
9.8000h / 1.002738 = 9.7732h
= 9h 46.4m丂UT
擔杮昗弨帪(+9h)偵曄姺
弌尰帪崗丂18h 46.4m JST
杤帪崗乮峆惎偑杤偡傞抧曽峆惎帪乯
兛 + h0 + 嚈H
= 6h 45.1m + 5h 11.4m + 0h 3.0m
= 11h 59.5m
峆惎偑杤偡傞抧曽峆惎帪傪悽奅帪UT傊曄姺
11h 59.5m=11.992h
15h 42.7m=15.712h
11.992h - 15.712h =-3.72h
亅乮儅僀僫僗乯偵側偭偨偨傔+24h
20.28h
20.280h / 1.002738 = 20.225h
= 20h 13.5m UT
擔杮昗弨帪(+9h)偵曄姺
29h 13.5m JST
杤帪崗丂1寧2擔丂5h 13.5m JST
峆惎偑弌杤偡傞曽埵A0
sinA0=-cos兟sin(h0 + 嚈H)
= -cos(-16亱43') x sin(亇(5h 11.4m + 0h 3.0m))
= - 0.95774 x (亇0.98027)
= 亇0.93884
弌尰帪丂0.93884
杤帪丂丂-0.93884
cosA0 = sin兟 / cos冋
= sin(-16亱43') / cos(35亱01')
= -0.28764/0.81898
= -0.35122
弌尰帪
cosA0丂亅丂丄sinA0丂亄丂偺偨傔戞俀徾尰
A0=110.14亱
杤帪
cosA0丂亅丂丄sinA0丂亅丂偺偨傔戞俁徾尰
A0=249.86亱
杒偐傜搶夞傝110.14亱偵偰弌尰偟丄249.86亱乮杒偐傜惣夞傝110.14亱乯偱杤偟傑偡丅
偙偺曽朄偱丄擔偺弌丄擔偺擖傝帪崗傕媮傔傞偙偲偑偱偒傑偡丅偙偺応崌丄抧媴偺婳摴梫慺偐傜懢梲偺愒宱丄愒堒傪媮傔傞昁梫偑偁傝傑偡丅偙傟偼彮偟柺搢偱偡偑丄師夞愢柧偟傛偆偲巚偄傑偡丅
偪側傒偵擔偺弌丄擔偺擖傝帪崗傪媮傔傞偵偼丄埲壓傪愢柧偡傞昁梫偑偁傝傑偡丅
抧暯帇嵎丄帇敿宎丄働僾儔乕偺曽掱幃丄榝惎偺婳摴梫慺丄擔怱捈岎嵗昗丄儀僋僩儖掕悢
屻丄揤暥寁嶼偵偼丄嵨嵎丄帇嵎偵偮偄偰偺峫偊曽偑昁梫偱偡丅
|

